EXPRESIONES ALGEBRAICAS

MATEMÁTICAS ACADÉMICAS Y APLICADAS

Política de privacidad y cookies

Condiciones de servicio

• 4.1 Expresiones algebraicas
  • Los polinomios
  • Suma y resta de polinomios
  • Producto de expresiones algebraicas
  • Productos notables

• 4.2 Factorización
  • Introducción
  • Factor Común
  • Identificación de productos notables
  • Factorización por la regla de Ruffini

• 4.3 Fracciones algebraicas
  • Introducción
  • Simplificación de fracciones algebraicas
  • Producto de fracciones algebraicas
  • División de fracciones algebraicas
  • Suma y resta de fracciones algebraicas
  • Fracciones compuestas
  • Racionalización de denominadores. Expresiones conjugadas.

En el cuarto apartado del curso online de Matemáticas de 4º de ESO ( Secundaría o Grado de Educación Media) iniciaremos el estudio de las expresiones algebraicas. Estas son operaciones de números con letras llamadas variables. Una variable es una letra que representa cualquier número dentro de cierto conjunto. Las expresiones algebraicas más sencillas son los polinomios, que estudiaremos a continuación.

Los polinomios son expresiones algebraicas que usan solo las operaciones de suma, resta y multiplicación. Constan de una suma de términos llamados monomios, que tienen forma         , donde a es el coeficiente (un número en general), x es la variable y n el exponente (el exponente de la variable) es el grado del monomio. El grado de un polinomio es el grado del término o monomio más alto de los que lo componen.

Veamos algunos ejemplos para aclarar estos conceptos:

• El polinomio                                 tiene tres términos o monomios. El grado del polinomio es 3. La variable es x.

•                                           es un polinomio de grado 7. Tiene 3 monomios. La variable es y.

•                                            es un polinomio de grado 4 y la variables es w.

Se llaman términos semejantes a términos que tienen las mismas variables elevadas a los mismos exponentes.

Los polinomios se suman y se restan usando un proceso llamado reducción de términos semejantes. Veamos como funciona con algunos ejemplos:

• Efectúa la suma siguiente: 

Primero agrupamos los términos semejantes, luego los reducimos sumando los coeficientes:

• Efectúa la siguiente diferencia:

Primero la transformamos en suma usando los opuestos de los coeficientes

Agrupamos los términos semejantes

Reducimos sumando los coeficientes

El producto de dos polinomios ( y en general de dos expresiones algebraicas) se realiza haciendo uso repetido de la propiedad distributiva. Cada término de uno de los polinomios se multiplica por todos los términos del otro. 

Veamos un ejemplo:

Ejemplo 1 - Calcula el siguiente producto: 

Calculamos los productos de cada término del primer polinomio por cada término del segundo:

Finalmente reducimos los términos semejantes:

Ejemplo 2 - Calcula el siguiente producto:

Reducimos los términos semejantes:

Hay una serie de productos que aparecen muy frecuentemente en los cálculos. Es aconsejable aprendérselos de memoria para reconocerlos cuando aparezcan:

• Diferencia de cuadrados:

• Cuadrado de una suma:

• Cuadrado de una diferencia:

Veamos cómo se aplican con unos ejemplos:

Ejemplo 1 - Desarrolla el siguiente paréntesis: 

Se trata del cuadrado de una diferencia, aplicamos la fórmula:

Ejemplo 2 - Desarrolla la siguiente expresión:

Es una suma por una diferencia, el resultado será una suma de cuadrados:

Llamamos factorización al proceso de escribir una expresión algebraica ( normalmente en forma de suma) como un producto de expresiones más simples. Éste es uno de los instrumentos más importantes del Álgebra. Es la operación inversa a desarrollar. En esta sección veremos las técnicas más importantes.

El factor común es la aplicación inversa de la propiedad distributiva:

Veamos alguno ejemplos de su utilización para poder entenderlo mejor:

• 1) Extrae factor común de la siguiente expresión:

Observa que en los dos términos de la expresión aparece el factor común X; lo ponemos fuera del paréntesis, y dentro del mismo la expresión sin el factor común:

• 2) Extrae factor común de :

En caso de duda podemos comprobar aplicando al resultado la propiedad distributiva.

• 3) Factoriza el siguiente polinómio:

El factor común más grande que se encuentra en los números ( 6, -2 y 8 ) es el 2; el factor común que se encuentra en los términos                                       .

Por tanto tendremos:

• 4) Extrae factor común de : 

El mayor factor común contenido en 4, -16 y 28 es 4.

El mayor factor común contenido en                     

El mayor factor común contenido en 

Por tanto, el factor común será                 , y obtendremos:

Las fórmulas que vimos en el apartado anterior sobre los productos notables nos pueden ayudar a factorizar expresiones que sean desarrollos perfectos de estos productos:

Veamos algunos ejemplos:

• 1) Factoriza:

Como         y 16 son los cuadrados perfectos de x y 4, comprobamos si el término media tiene la forma de un doble producto de x y 4:  2*x*4=8x. Efectivamente.

Finalmente el signo menos del doble producto indica que se trata del cuadrdo de una diferencia.

Por tanto:

• 2) Factoriza:

El primer término de la expresión es el cuadrado de 5x y el segundo término es el cuadrado de 8. Así pues, tenemos una diferencia de cuadrados, y su descomposición factorial será:

• 3) Factoriza:

    es el cuadrado de 3x; 4 es el cuadrado de 2. Además, el término central es el doble del producto 2*3x*2=12x. Tenemos por tanto que el polinomio es el cuadrado de una suma:

Algunas veces tendremos que combinar este método con la extracción del factor común.

Veamos unos ejemplos:

• 1) Factoriza:

Primero sacamos factor común de          :

El término que está entre paréntesis es el cuadrado de una suma, por tanto:

• 2) Factoriza:  

Primero sacamos factor común de 3:

Observamos que el término entre paréntesis es una diferencia de cuadrados.

La descomposición será:

Una vez descartados los dos procedimientos anteriores todavía podemos intentar la descomposición del polinomio utilizando la división por la Regla de Ruffini. Cuando esta división es exacta (el resto da cero), podemos expresar el polinomio dividendo como el producto del polinomio cociente por el polinomio divisor. 

• 1) Factoriza: 

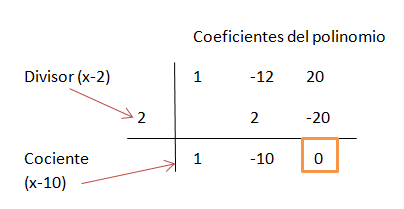
Al dar cero la división, tenemos que:

• 2) Factoriza:

Aquí la división da cero para -2:

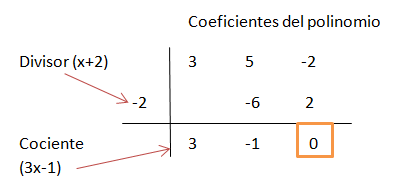
Por tanto:

• 3) Factoriza:

Sacamos factor común 8:

Ahora descomponemos el polinomio del paréntesis utilizando el método de Ruffini:

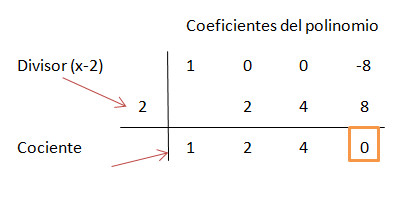
Observa que hemos añadido ceros en el polinomio para completar los términos que faltan.

La descomposición será por tanto la siguiente:

Llamamos fracción algebraica al cociente de dos expresiones algebraicas. En esta sección vamos a revisar las operaciones usuales de este tipo de fracciones.

Simplificaremos  las fracciones algebraicas del mismo modo que simplificamos las fracciones de números. Primero factorizaremos el numerador y el denominador, y luego eliminaremos los factores comunes que existan.

Veamos algunos ejemplos:

• 1) Simplifica:

Primero factorizamos el numerador y el denominador:

Después eliminamos el factor (x-1):

El producto de fracciones algebraicas también se realiza de acuerdo con la misma regla para multiplicar fracciones numéricas:

Sin embargo, antes de multiplicar numeradores y denominadores, primero los factorizaremos y simplificaremos eliminando los factores comunes. Por último, realizaremos la multiplicación de las expresiones que queden.

Veamos un ejemplo:

• Multiplica las siguientes fracciones:

Primero factorizamos cada una de las expresiones:

Ahora realizamos la multiplicación y simplificamos los factores comunes del numerador y el denominador:

Para realizar la división de fracciones algebraicas, usaremos la regla de la división de fracciones numéricas. Primero se invierte la segunda fracción y después se multiplican:

Veamos un ejemplo:

• Divide las siguientes fracciones:

Primero invertimos la segunda fracción y escribimos el símbolo de multiplicación:

Ahora factorizamos cada una de las expresiones:

Cancelamos los términos comunes:

• Divide las fracciones:

Invertimos y multiplicamos:

Factorizamos:

Simplificamos los términos comunes:

Al igual que en las fracciones numéricas, para realizar la suma y resta de fracciones algebraicas, sus denominadores deben ser iguales.

Veamos algunos ejemplos:

• Efectúa la siguiente suma:

El m.c.m de ( x + 3 ) y ( x + 5 ) es [(x+3)*(x+5)]

Observa que hemos sumado los términos del numerador pero hemos dejado factorizado el denominador.

• Efectúa la siguiente suma:

El m.c.m de (x-3), (x+2) y (x+3) es (x+2)(x+3)(x-3), por tanto:

• Calcula: 

Comenzamos descomponiendo en factores los denominadores:

Resolvemos

Para simplificar una fracción algebraica compuesta, trabajaremos por separado en el numerador y en el denominador de la fracción para conseguir fracciones simples. Después dividiremos estas dos fracciones.

Veamos algunos ejemplos:

• Calcula:

Numerador:

Denominador:

Por tanto:

Recordaremos que la racionalización era un proceso por el cual eliminábamos las raíces del denominador de una fracción. Esto se conseguía multiplicando el denominador y el numerador por una expresión adecuada.

En el caso de que en el denominador haya una suma o diferencia de raíces, la expresión apropiada para multiplicar es su expresión conjugada. Por ejemplo, la expresión conjugada de ( a + b ) es ( a - b ). Es decir, si tenemos una suma su expresión conjugada es la resta correspondiente.

Observemos que si multiplicamos una expresión por su conjugada obtenemos una diferencia de cuadrados:

Esta propiedad es la que nos va a permitir racionalizar el denominador cuando haya una suma o resta de raíces.

Veamos algunos ejemplos:

• Racionaliza el denominador de la siguiente expresión:

Multiplicaremos los dos términos de la fracción por el conjugado del denominador:

• Racionaliza la expresión:

La expresión conjugada de                                                . Multiplicaremos los dos términos de la fracción por esta expresión:

Isabel - Profe Online

Clases particulares de Matemáticas, Física y Química